Modifiers

Regular Expression modifiers are special characters which change how sub-expressions of the regex are interpreted. The three modifiers we’ll be implementing will be the '?', '+', and '*' modifiers.

Expected Behavior of Modifiers

Zero or One

The '?' symbol is the ‘Zero or One’ modifier. It says that the regex should match an expression if it appears zero or once. For example, the regular expression ab?c has the following match profile;

• 'abc' → match
• 'ac' → match
• 'abbc' → no match

Similarly, the regular expression (abc)?z has the profile

• 'abcz' → match
• 'z' → match
• 'abcabcz' → no match

One or More

The '+' symbol is the ‘One or More’ modifier. It says that the regex should match an expression if it appears one or more times. For example, the regular expression ab+c has the following match profile;

• 'abc' → match
• 'abbc' → match
• 'abbbc' → match
• 'ac' → no match

Similarly, the regular expression (abc)+ has the profile

• 'abc' → match
• 'abcabc' → match
• '' → no match

Zero or More

The '*' symbol is the ‘Zero or More’ modifier. It says that the regex should match an expression if it appears zero or more times. For example, the regular expression ab*c has the following match profile;

• 'abc' → match
• 'abbc' → match
• 'abbbc' → match
• 'ac' → match

Similarly, the regular expression `(abc)*’ has the profile

• 'abc' → match
• 'abcabc' → match
• '' → match

Modelling Modifiers with Epsilon FSMs

Modelling this behaviour with state machines is fairly straight forward when using epsilon transitions.

Let’s start with the Zero or One modifier.

Zero or One

Modelling the behaviour for this modifier involves implementing an optional skip step between the State (or States) that represent the sub expression, so that we can ‘skip’ over it for the ‘zero’ case or pass through it as normal for the ‘one’ case.

This should look something like this;

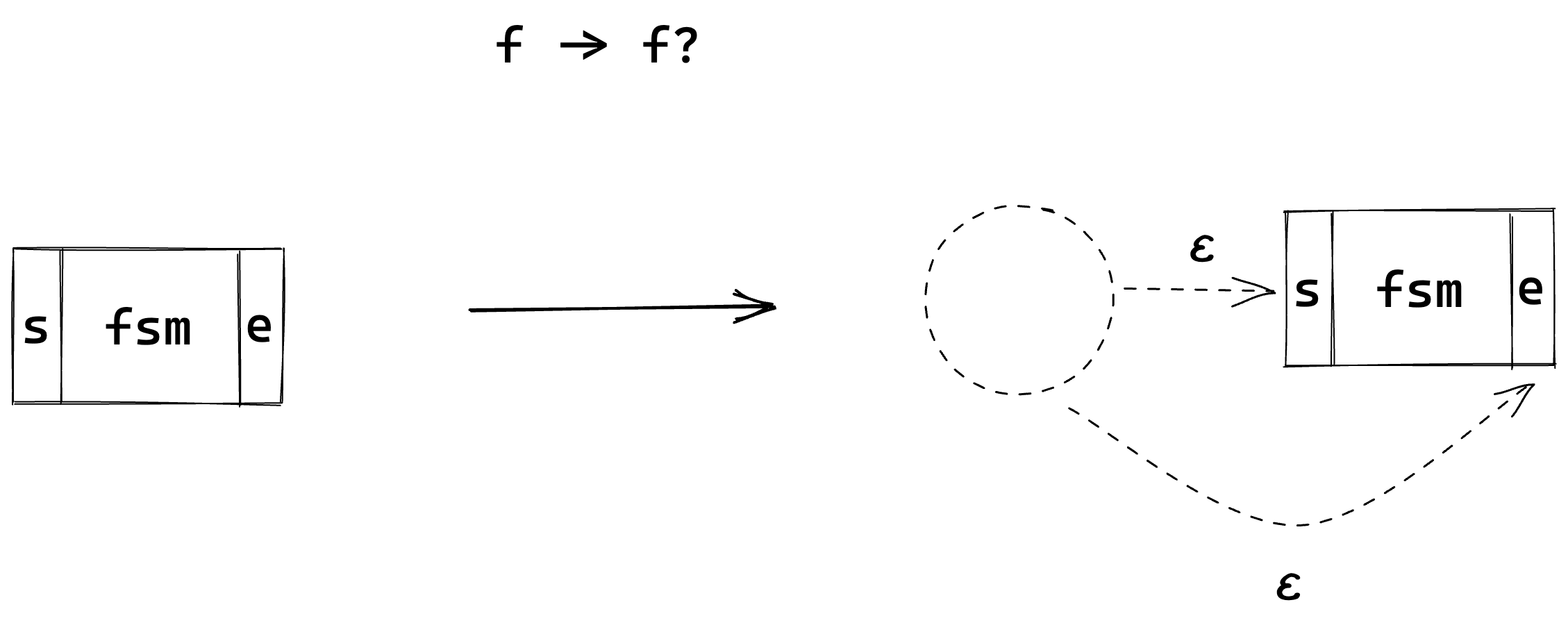
Let’s explain this a bit.

To apply the '?' modifier to an FSM, we need to start from a State which has an epsilon transition to the start of the FSM, and also an epsilon transition to the end of the FSM.

The epsilon transition to the start of the FSM represents the ‘one’ case, in which we walk as normal through the FSM.

The epsilon transition to the end of the FSM represents the ‘zero’ case, in which we skip the FSM entirely.

For example, the regex dogs? would look like so;

And (dog)?s would be;

One Or More

The One or More modifier will involve an optional loop. The loop will be used to represent the ‘or More’ case, and will involve looping back from the end of the sub expression back to the beginning. This can happen as many times as necessary, because the sub expression can be matches any number of times.

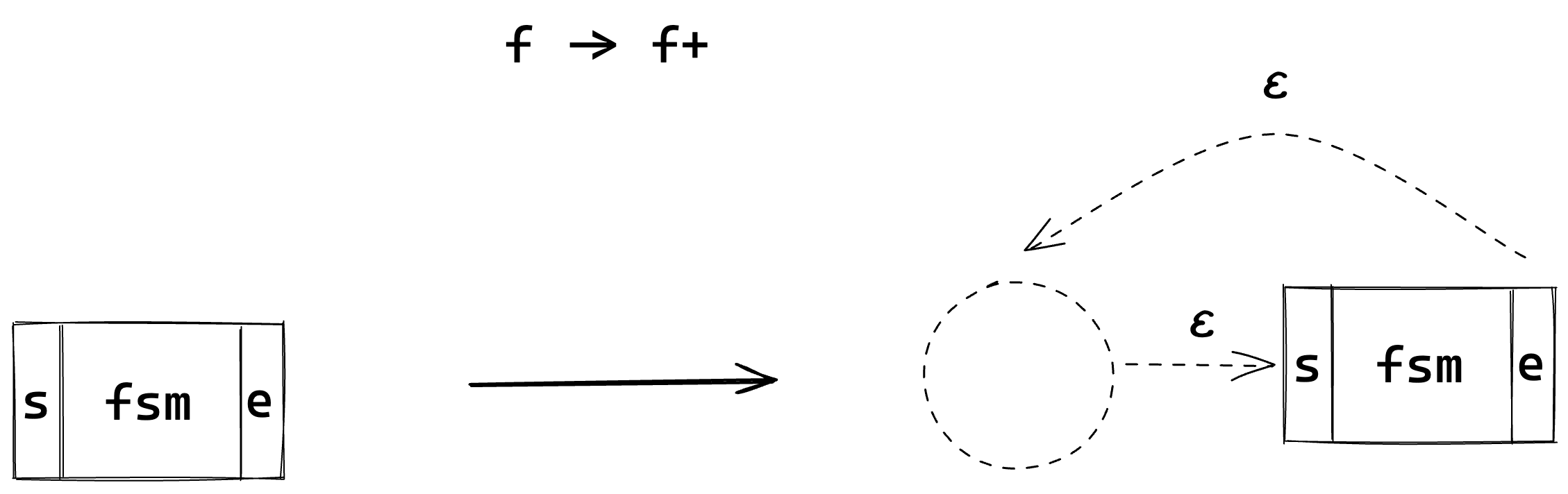
It should be clear that this looks very similar to the Zero Or One case.

The ‘One’ case is still the same, so we still need our epsilon transition pointing to the start of the FSM sub expression so that we can walk through the FSM as usual.

The loop for the ‘Or More’ case is implemented with an epsilon transition pointing from the end of the FSM back to the start¹. This means that we can walk through the FSM sub expression as many times as we want without it failing.

To use the same examples as before, the regex dogs+ would look like so;

And (dog)+s would be;

It might be worth stepping through these examples in your head. Although the difference in the FSM graphs is visually subtle, the effect is significant.

Zero or More

The ‘Zero or More’ modifier can actually be composed of the ‘One or More’ and ‘Zero or One’ modifiers.

We need both the skip for the ‘Zero’ case, and the loop from the ‘or More’ case.

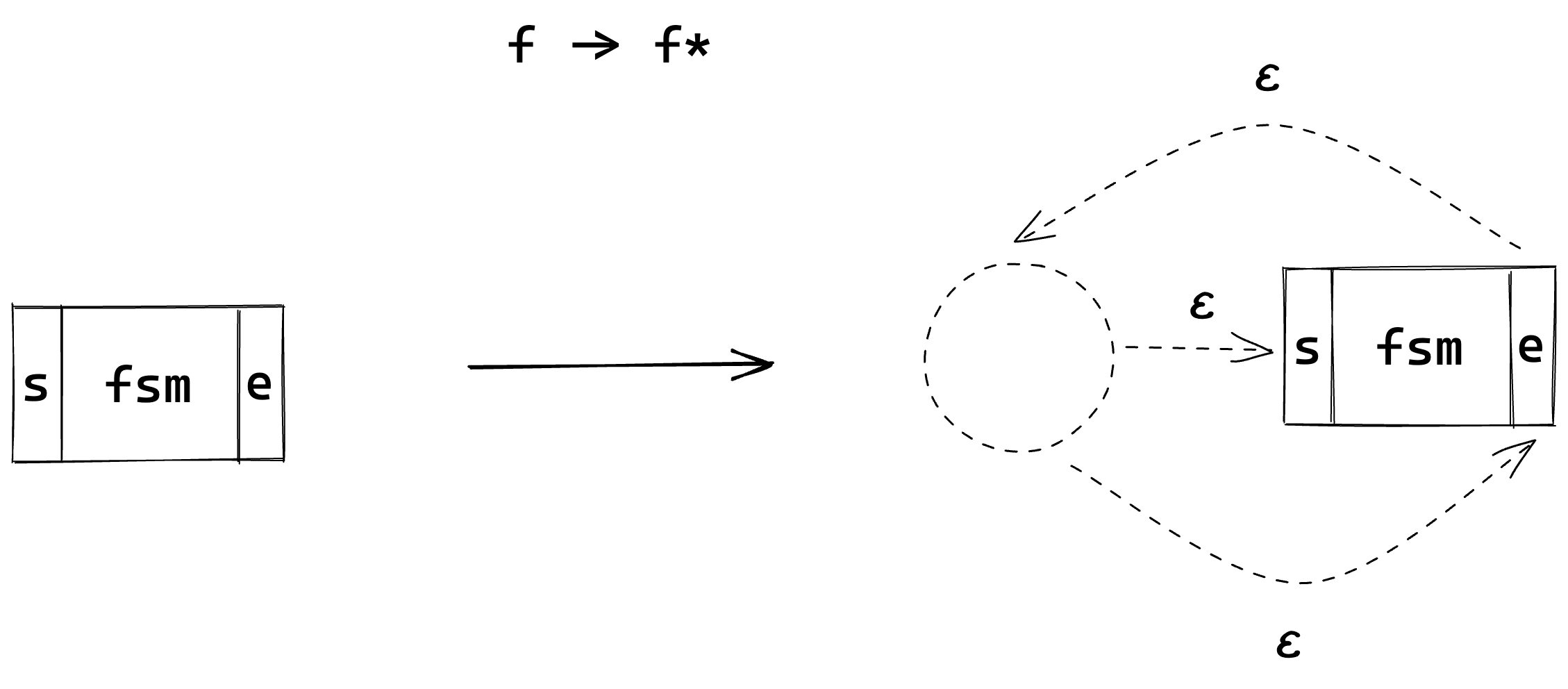
Again, the regex dogs* would look like so;

And (dog)*s would be;

Composing these FSMs with epsilons is a lot easier than without them.

Why Epsilons?

As a quick aside, it’s worth noting here that it might seem that the epsilon transitions make things more complicated rather than more simple. For example, the regex (dog)*s can be constructed without epsilons. Actually, all epsilon FSMs can be constructed as non-epsilon FSMs. Let’s take a look at what such an FSM might look like.

This is still fairly simple, but we need to know a few things about the FSM sub expression in order to construct it, such as the transitions to and from the start and end states. The nice thing about epsilon transitions is that you can ignore the inner details of the sub expressions.

Implementing Modifiers

Now we know the theory, let’s start adding modifiers to our system.

Parser

Let’s start with our modifier data structures.

// ast.go

type ZeroOrOneModifier struct {  
   Child Node  
}  
  
type OneOrMoreModifier struct {  
   Child Node  
}  
  
type ZeroOrMoreModifier struct {  
   Child Node  
}

And we’ll add a simple string() method to them for debugging purposes.

// ast.go

func (zo ZeroOrOneModifier) string(indentation int) string {  
   return compositeToString("ZeroOrOne", []Node{zo.Child}, indentation+1)  
}  
  
func (om OneOrMoreModifier) string(indentation int) string {  
   return compositeToString("OneOrMore", []Node{om.Child}, indentation+1)  
}  
  
func (zm ZeroOrMoreModifier) string(indentation int) string {  
   return compositeToString("ZeroOrMore", []Node{zm.Child}, indentation+1)  
}

As well as some a stand in compile() method so that the compiler doesn’t complain.

// ast.go
  
func (zo ZeroOrOneModifier) compile() (head *State, tail *State) {  
   panic("implement me")
}  
  
func (om OneOrMoreModifier) compile() (head *State, tail *State) {  
   panic("implement me") 
}  
  
func (zm ZeroOrMoreModifier) compile() (head *State, tail *State) {  
   panic("implement me")
}

Now that we have our data structures, let’s set up some simple tests for the parser.

@@ // parser_test

@@ func TestParser(t *testing.T) {
+               {
+                       name:  "zero or one modifier on a character",
+                       input: "a?",
+                       expectedResult: &Group{ChildNodes: []Node{
+                               ZeroOrOneModifier{Child: CharacterLiteral{Character: 'a'}},
+                       }},
+               },
+               {
+                       name:  "zero or one modifier on a group",
+                       input: "(ab)?",
+                       expectedResult: &Group{ChildNodes: []Node{
+                               ZeroOrOneModifier{Child: &Group{ChildNodes: []Node{
+                                       CharacterLiteral{Character: 'a'},
+                                       CharacterLiteral{Character: 'b'},
+                               }}},
+                       }},
+               },
+               {
+                       name:  "one or more modifier on a character",
+                       input: "a+",
+                       expectedResult: &Group{ChildNodes: []Node{
+                               OneOrMoreModifier{Child: CharacterLiteral{Character: 'a'}},
+                       }},
+               },
+               {
+                       name:  "one or more modifier on a group",
+                       input: "(ab)+",
+                       expectedResult: &Group{ChildNodes: []Node{
+                               OneOrMoreModifier{Child: &Group{ChildNodes: []Node{
+                                       CharacterLiteral{Character: 'a'},
+                                       CharacterLiteral{Character: 'b'},
+                               }}},
+                       }},
+               }, {
+                       name:  "zero or more modifier on a character",
+                       input: "a*",
+                       expectedResult: &Group{ChildNodes: []Node{
+                               ZeroOrMoreModifier{Child: CharacterLiteral{Character: 'a'}},
+                       }},
+               },
+               {
+                       name:  "zero or more modifier on a group",
+                       input: "(ab)*",
+                       expectedResult: &Group{ChildNodes: []Node{
+                               ZeroOrMoreModifier{Child: &Group{ChildNodes: []Node{
+                                       CharacterLiteral{Character: 'a'},
+                                       CharacterLiteral{Character: 'b'},
+                               }}},
+                       }},
+               },

As we can see from our tests, the modifier structs act as wrappers around a single Child inner Node.

Implementing this in our parser is fairly straight forward. We simply need to use a wrapper function, which will wrap the node if there is a modifier character present.

@@ // parser.go

@@ func (p *Parser) Parse(tokens []token) Node {
        for i, t := range p.tokens {
                switch t.symbol {
                case Character:
                        node := p.pop()
-                       node.Append(CharacterLiteral{Character: t.letter})
+                       node.Append(p.wrapWithModifier(i, CharacterLiteral{Character: t.letter}))
                        p.push(node)
                case AnyCharacter:
                        node := p.pop()
-                       node.Append(WildcardLiteral{})
+                       node.Append(p.wrapWithModifier(i, WildcardLiteral{}))
                        p.push(node)
@@				[...]
                case RParen:
                        inner := p.pop()
                        outer := p.pop()
-                       outer.Append(inner)
+                       outer.Append(p.wrapWithModifier(i, inner))
                        p.push(outer)
                }
        }

The wrapper function is p.wrapWithModifier(). let’s take a look at it’s implementation.

// parser.go

func (p *Parser) peekAhead(i int) (bool, token) {  
   nextIndex := i + 1  
  
   if nextIndex >= len(p.tokens) {  
      return false, token{}  
   }  
  
   return true, p.tokens[nextIndex]  
}  
  
func (p *Parser) wrapWithModifier(i int, child Node) Node {  
   ok, nextToken := p.peekAhead(i)  
   if ok {  
      switch nextToken.symbol {  
      case ZeroOrOne:  
         return ZeroOrOneModifier{Child: child}  
      case OneOrMore:  
         return OneOrMoreModifier{Child: child}  
      case ZeroOrMore:  
         return ZeroOrMoreModifier{Child: child}  
      }  
   }  
  
   return child  
}

We use peekAhead() to check if there’s a modifier token next, and if there is, we wrap the Node in the correct modifier. Otherwise, we return the Node as is.

Now the parser tests are passing, let’s move onto the compiler.

Compiler

Let’s start with some tests;

@@ // fsm_test.go

@@ func TestFSMAgainstGoRegexPkg(t *testing.T) {
                {"word followed by group", "1(|)", "0"},
                {"empty group concatenation", "(()0)0", "0"},
                {"group followed by word", "(|)1", "0"},
+
+               // zero or one
+               {"simple zero or one with 0 '?' match", "ab?c", "ac"},
+               {"simple zero or one with one '?' matches", "ab?c", "abc"},
+               {"simple zero or one too many '?' matches", "ab?c", "abbc"},
+
+               // one or more
+               {"simple one or more with 0 '+' matches", "ab+c", "ac"},
+               {"simple one or more with one '+' matches", "ab+c", "abc"},
+               {"simple one or more with many '+' matches", "ab+c", "abbbbc"},
+
+               // zero or more
+               {"simple zero or more with 0 '*' matches", "ab*c", "ac"},
+               {"simple zero or more with one '*' matches", "ab*c", "abc"},
+               {"simple zero or more with many '*' matches", "ab*c", "abbbbc"},
        }

And now we simply need to implement the compile() methods. Let’s start with ZeroOrOneModifier.

// ast.go

func (zo ZeroOrOneModifier) compile() (head *State, tail *State) {  
   startState := &State{}  
   endState := &State{}  
  
   head, tail = zo.Child.compile()  
  
   // 'one' case, go through expression as normal  
   startState.addEpsilon(head)  
   // 'zero' case, skip to end of expression  
   startState.addEpsilon(tail)  
  
   tail.addEpsilon(endState)  
   return startState, endState  
}

Following our designs above, the ZeroOrOneModifier will create a new State with the name startState, and add an epsilon transition from startState to the first ‘head’ State of the compiled Child inner Node. This is for the ‘one’ case.

We also need to add an epsilon transition from StartState to the last ’tail’ State of the compiled Child inner Node, to represent the zero case where we simply ‘skip’ to the end.

You’ll notice that we also add an extra State called endState, which we link to the ’tail’ state of the compiled Child inner Node. This is not strictly necessary here, but it will ensure that our trick of saying that any State without outgoing transitions is a success State will continue to work, even if we add epsilon transitions to the last ’tail’ State.

Let’s do the same for OneOrMoreModifier.

// ast.go

func (om OneOrMoreModifier) compile() (head *State, tail *State) {  
   startState := &State{}  
   endState := &State{}  
  
   head, tail = om.Child.compile()  
  
   // 'one' case, go through expression as normal  
   startState.addEpsilon(head)  
   // 'more' case, loop back through the expression  
   tail.addEpsilon(startState)  
  
   tail.addEpsilon(endState)  
   return startState, endState  
}

Here we don’t need the ‘zero’ case, but we need a ‘more’ case in which we loop back from the last ’tail’ State back to the startState.

And now for the ZeroOrMoreModifier.

// ast.go

func (zm ZeroOrMoreModifier) compile() (head *State, tail *State) {  
   startState := &State{}  
   endState := &State{}  
  
   head, tail = zm.Child.compile()  
  
   // 'one' case, go through expression as normal  
   startState.addEpsilon(head)  
   // 'more' case, loop back through the expression  
   tail.addEpsilon(startState)  
   // 'zero' case, skip to end of expression  
   startState.addEpsilon(tail)  
  
   tail.addEpsilon(endState)  
   return startState, endState

Here we need the ‘one’, ‘more’ and ‘zero’ cases.

With those changes, our tests should be passing! Let’s try out a few examples with our command line.

A few examples

Let’s first try with the regular expression ca(rro)?t using the Zero or One modifier.

We can see in this example that when matching the (rro) sub expression, the matcher travels along the bottom row of States.

When not matching the sub expression, the matcher uses the epsilons to go straight past the sub expression.

Let’s try something similar with the ‘One or More’ modifier.

In this example, the regex I( love)+ cats is a good demonstration of the ‘More’ case looping over every match of the ( love) sub expression.

And for one more example, let’s combine the wildcard '.' symbol with the Zero or More * symbol to create a generic matcher for any substring.

Now that we can combine and compose modifiers and branches, we can create some really sophisticated regular expression matchers. Let’s look at an example where we combine all of the components we’ve created so far.

There are a lot of moving parts here, but our composable design is keeping things in check.

Let’s make sure that everything is working as expected by running our fuzzer. First, remove *+? from our special character filter.

@@ // fsm_test.go

@@ func FuzzFSM(f *testing.F) {
        f.Fuzz(func(t *testing.T, regex, input string) {
-               if strings.ContainsAny(regex, "[]{}$^*+?\\") {
+               if strings.ContainsAny(regex, "[]{}$^\\") {

Then, we’ll also need to check for regular expressions where ? is used on its own, as this is used for group constructions which we’re not implementing in this project.

@@ // fsm_test.go

@@ func FuzzFSM(f *testing.F) {
                if strings.ContainsAny(regex, "[]{}$^\\") {
                        t.Skip()
                }
+               if strings.Contains(regex, "(?") {
+                       // '?' on its own is used for special group constructs, which we're not implementing.
                        t.Skip()
                }

The fuzzer should now be able to fun without finding any errors!

What’s next?

There are many more features of modern regex engines which we could implement. For example, we could allow regular expressions with {3} which would match exactly 3 sub expressions. Or we could allow character ranges such as [a-zA-Z]. We could match on expressions which start or end with an expression using ^ and $.

We could also extend our matcher by returning the substring indices of the match, or by accounting for match groups.

There’s also a myriad of performance improvements we could make - our implementation is currently many, many orders of magnitude slower than the Golang implementation…

However, what I’m more interested in is converting our epsilon-based NFA to a DFA, in which every State has only one valid Transition per input.

After that, I’ll probably call it a day with this project (unless something else perks my curiosity - I’m open to suggestions!).