Making regex from scratch in go
02 Getting into some code
Let’s start coding.
The FSM data structure
We can first think about our core data structures to represent the FSM. The FSM is essentially a linked list of state objects.
// state.go
type State struct {
connectedStates []*State
}
We need a bit more information, however, as we need to know which character allows us to go from one state to another. We’ll use a Transition struct to represent this.
The Transition struct contains two things:
- the next state
- the predicate that determines whether we can go to the next state
// transition.go
type Transition struct {
to *State
from *State
predicate Predicate
}
The Predicate is a simple function that takes in a character.
here we’re using rune to avoid multi-byte character issues.
// transition.go
type Predicate func(input rune) bool
To put this all together, let’s make some changes to our State struct definition in order to use our Predicate and Transition types.
@@ // state.go
type State struct {
- connectedStates []*State
+ transitions []Transition
}
Running Our State machine
In order to use our state machine, we’ll need something that can process a string by running through the states, and that can give information on matches. As this is an object that runs through our state machine, we’ll call this a Runner.
// runner.go
type runner struct {
head *State
current *State
}
For now, all our runner needs to have is a pointer to the root (or head) node of our FSM, as well as another pointer which tracks where we are in the state machine (the red dot in our diagrams).
Tests first
We’ll be following TDD principles when convenient in order to make sure things are working as expected (and because, personally, I find it more fun). As we now have our fundamental objects mapped out, we can now start writing some tests.
Our first test will check the behaviour of a simple FSM which represents the regex expression abc. The first thing to do is construct the FSM. We’ll do this ‘by hand’ for now, and later we’ll work on a compiler that can take a string like "abc" and build an FSM automatically.
// fsm_test.go
func TestHandmadeFSM(t *testing.T) {
startState := State{}
stateA := State{}
stateB := State{}
stateC := State{}
startState.transitions = append(startState.transitions, Transition{
to: &stateA,
predicate: func(input rune) bool { return input == 'a' },
})
stateA.transitions = append(stateA.transitions, Transition{
to: &stateB,
predicate: func(input rune) bool { return input == 'b' },
})
stateB.transitions = append(stateB.transitions, Transition{
to: &stateC,
predicate: func(input rune) bool { return input == 'c' },
})
}
There’s quite a bit going on here, so let’s break it down a bit.
First, let’s remind ourselves of the FSM structure for the regex abc
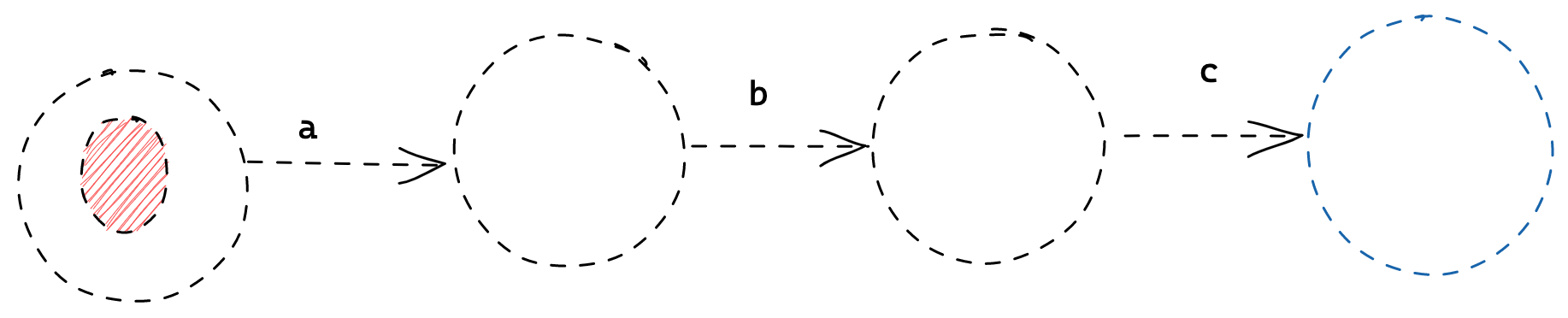
There are 4 states which we have to define first.
startState := State{}
stateA := State{}
stateB := State{}
stateC := State{}
Once we have our states, we need to describe the transitions between them. The first is the transition from the startState to stateA. To do this, we simply append a Transition object to the transitions property of startState. This new transition must point to stateA, and take as it’s predicate a function that returns true if the input rune is 'a'.
// fsm_test.go
startState.transitions = append(startState.transitions, Transition{
to: &stateA,
predicate: func(input rune) bool { return input == 'a' },
})
The same goes for the remaining states.
// fsm_test.go
stateA.transitions = append(stateA.transitions, Transition{
to: &stateB,
predicate: func(input rune) bool { return input == 'b' },
})
stateB.transitions = append(stateB.transitions, Transition{
to: &stateC,
predicate: func(input rune) bool { return input == 'c' },
})
We now have our first FSM starting at the root node startState. Let’s write a test which creates a runner and uses this FSM to check against a few different input cases.
The outcome of running a string through an FSM should result in one of 3 statuses;
Normal. The FSM has not found a match yet, but neither has it found that there is no match. Another way of saying this is that the search is still ‘in progress’.Success. The FSM has found a match.fail. The FSM has found that the string does not match.
We can define these as constants of a specific type.
// state.go
type Status string
const (
Success Status = "success"
Fail = "fail"
Normal = "normal"
)
With that in mind, we can think of a few cases to test our FSM and runner logic;
""→normal"xxx"→fail"abc"→success"ab"→normal
Writing these up into table-style tests, we get the following;
// fsm_test.go
type test struct {
name string
input string
expectedStatus Status
}
tests := []test{
{"empty string", "", Normal},
{"non matching string", "x", Fail},
{"matching string", "abc", Success},
{"partial matching string", "ab", Normal},
}
The actual tests should simply create a runner using our hand-made FSM, iterate through the runes in the input string, and check that the Status of the runner is the same as our expected status.
// fsm_test.go
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
runner := NewRunner(&startState)
for _, character := range tt.input {
runner.Next(character)
}
result := runner.getStatus()
if tt.expectedStatus != result {
t.Fatalf("Expected FSM to have final state of '%v', got '%v'", tt.expectedStatus, result)
}
})
}
Notice that we had to invent a couple of methods to make this work, such as the NewRunner, runner.Next and runner.getStatus. This is fine, as we’ll come back to implementing these in a moment.
All together, our first test looks like this;
// fsm_test.go
func TestHandmadeFSM(t *testing.T) {
// hand-made FSM
startState := State{}
stateA := State{}
stateB := State{}
stateC := State{}
startState.transitions = append(startState.transitions, Transition{
to: &stateA,
predicate: func(input rune) bool { return input == 'a' },
})
stateA.transitions = append(stateA.transitions, Transition{
to: &stateB,
predicate: func(input rune) bool { return input == 'b' },
})
stateB.transitions = append(stateB.transitions, Transition{
to: &stateC,
predicate: func(input rune) bool { return input == 'c' },
})
type test struct {
name string
input string
expectedStatus Status
}
tests := []test{
{"empty string", "", Normal},
{"non matching string", "xxx, Fail},
{"matching string", "abc", Success},
{"partial matching string", "ab", Normal},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
runner := NewRunner(&startState)
for _, character := range tt.input {
runner.Next(character)
}
result := runner.getStatus()
if tt.expectedStatus != result {
t.Fatalf("Expected FSM to have final state of '%v', got '%v'", tt.expectedStatus, result)
}
})
}
}
One might take a look at this test and say, “The states are being instantiated once and then used in every test. This is a bad practice as one test might affect the outcome of another.” and I would totally agree. The only reason we’re getting away with it here is because our State Machines are stateless, meaning they don’t contain any information about the state of the process. On the other hand, our runner instance is stateful, so we want to create a new instance for every test case.
Now that we have our first test, let’s implement the missing methods and make these tests pass.
Runner
The first method we need to implement is a simple constructor function.
// runner.go
func NewRunner(head *State) *runner {
r := &runner{
head: head,
current: head,
}
return r
}
This is a simple constructor which requires that we store two pointers to the root State. The head state will remain constant in case we want to reset the runner. The current state will represent where we are in the FSM, as represented by the red dot in our state machine diagrams.
This assumes that we can only be in one place at a time in our FSM, more on that later..
Now, the Next method.
// runner.go
func (r *runner) Next(input rune) {
if r.current == nil {
return
}
// move to next matching transition
r.current = r.current.firstMatchingTransition(input)
}
All this does is change the r.current state to the state pointed to by the first matching transition of the current state. If r.current is nil, that means that the FSM has already fallen into a fail state, and so should do nothing.
The logic for finding the first matching transition is implemented on a method of the State struct, so let’s implement that now.
// state.go
func (s *State) firstMatchingTransition(input rune) *State {
for _, t := range s.transitions {
if t.predicate(input) {
return t.to
}
}
return nil
}
This is also pretty simple. The function loops over the transitions of the state and returns the to state of the first transition, which passes the predicate test function. Notice that if the state has no transition which matches the predicate, the function returns nil - this is the same as the red dot in our diagrams leaving the FSM and represents a Fail case.
Finally, we just need to determine the status of the FSM at any time.
// runner.go
func (r *runner) GetStatus() Status {
// if the current state is nil, return Fail
if r.current == nil {
return Fail
}
// if the current state has no transitions from it, return Success
if r.current.isSuccessState() {
return Success
}
// else, return normal
return Normal
}
Again, the logic for determining a Success status is implemented as a State struct method.
// state.go
func (s *State) isSuccessState() bool {
if len(s.transitions) == 0 {
return true
}
return false
}
Here we’re making an assumption; if a transition leads to no other states, we can consider it a success state. This is not strictly true, but it’s useful for now.
If we run the tests again, they should now be green! We now have a working, although pretty simple, finite state machine regex processor!
Check out this part of the project on github here
Previous: 01 Intro
Next: 03 Starting the compiler