So, one of the things I’ve wanted to play around with is search and regex. Searching through text for matches to a regular expression can be efficiently implemented using finite state machines.

Finite State Machines

Finite state machines are both simple and useful. The simplest definition I can think of is something like this:

A finite State Machine (FSM) is a series of states. The machine start in some state, then decides the next state to go to based on some input.

One of the cool things about FSMs is that they can be drawn as lovely little circles and arrows representing states and transitions:

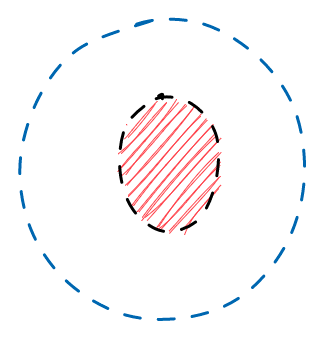
This is the simplest. It’s just a single state. The red circle in the middle means that we’re currently in that state, although that doesn’t tell us much yet…

For this to be useful, we need more than one state.

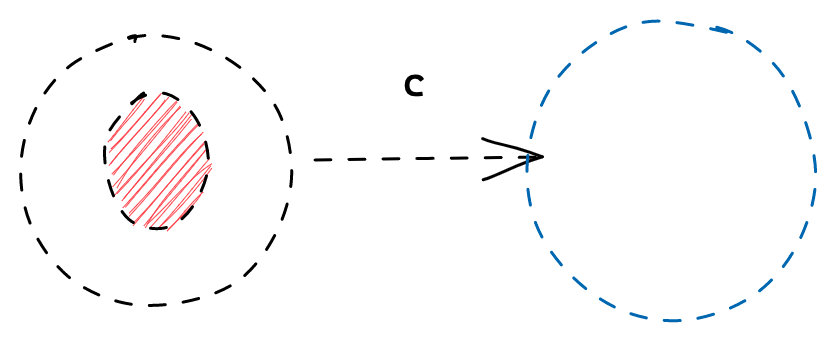
This a two state system. Starting from the state on the left - we’ll call it state[0] - we travel to the state on the right - state[1] - only if we see the character c.

Two things to note here:

1. What happens if we process a different character to c, such as z? From the picture, we don’t know what to do as there is no arrow for the z case. To be truly accurate, we would need to have an arrow for every possible character. For brevity, let’s say that if there is no arrow, there was no match.
2. The circle on the right is blue. This means this is an end state. If we arrive at this state we have finished and a match has been found.

This is all lovely, but what can we actually do with this? We’re going to use these machines to solve regular expressions.

Text search

Let’s create a state machine which checks if a string matches against a simple regular expression query abc. This means that any string containing the substring abc will match. For example:

• "zabcz" -> match
• "abc" -> match
• "abd" -> no match
• "" -> no match

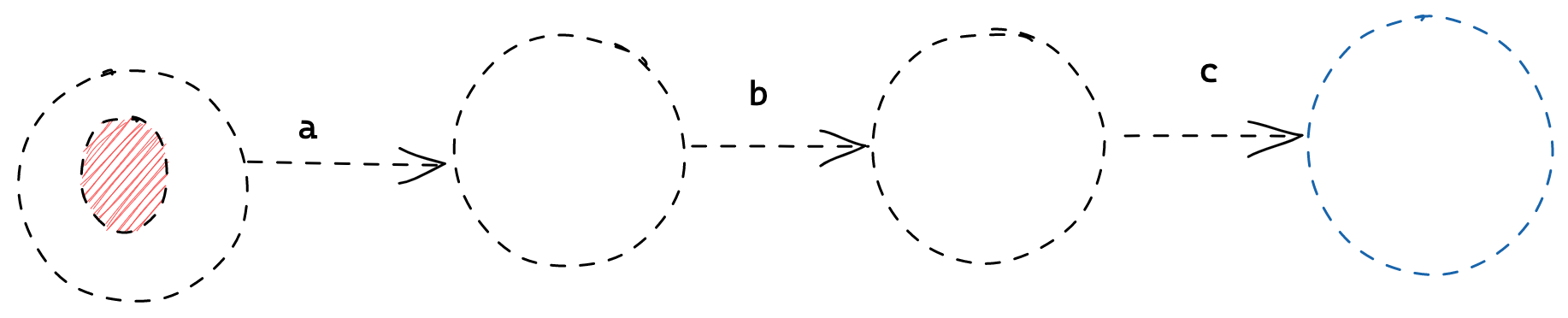
The finite state machine which represents this regular expression is as follows:

let’s break this down a bit. Really, each state is saying something.

State 0 is saying: “you have not yet seen anything interesting” State 1 is saying: “you’ve just seen 'a'” State 2 is saying: “you’ve just seen 'ab'” State 3 is saying “you’ve just seen 'abc' so you’re done!”

Let’s get into these states and what they’re saying a little more to try to understand all of these arrows.

At state 0, I still haven’t seen anything interesting until I see an 'a', that’s pretty straight forward.

At state 1, I know that the first character I saw as 'a'

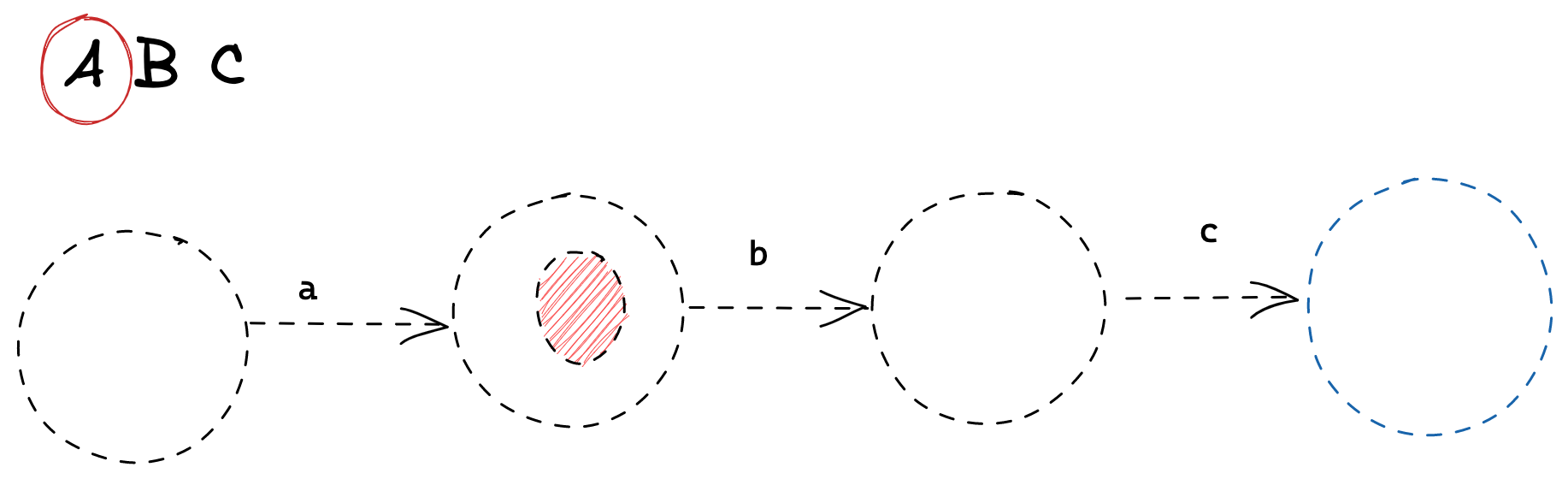
At state 2 we’re saying “you’ve just seen 'ab'.

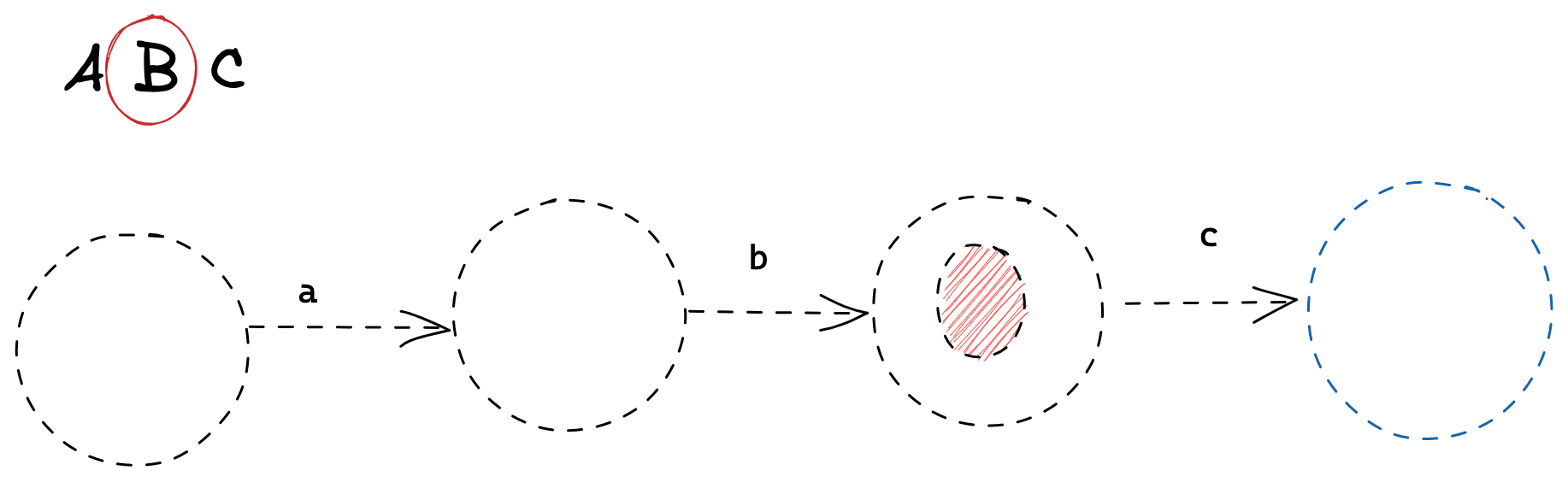
And at state 3, we know we’ve seen 'abc', so we don’t want to do anything from here!

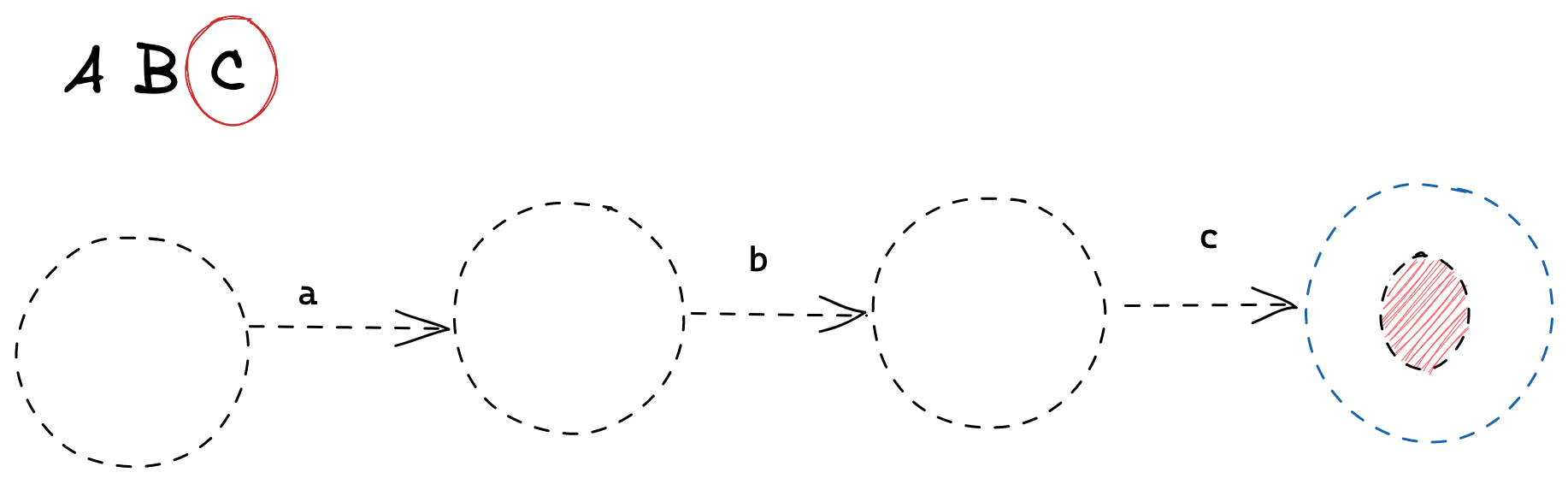
That’s really all there is to it. The interesting thing is how we can combine arrows and circles to create FSM that can represent complex regular expressions.